Practice
Practical Applications
There are several applications that require new theoretical approaches and new methods of modeling. These include the age crime curve, the propensity-sanctioning dilemma, and the prediction problem. By using a bivariate probit model of propensity, sanctioning, and crime with multiple time varying covariates, it is possible to solve these complex problems.
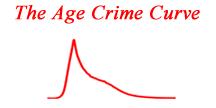
Application #1: The Age Crime Curve Puzzle
One of the enduring puzzles in criminology is the age crime curve. why does crime start at near zero in childhood, rise to a peak in late adolescence, and then drop to near zero in old age? The solution to this problem requires a new theory and new methods.
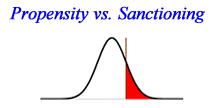
Application #2: The Propensity-Sanctioning Dilemma
Another enduring problem in criminology is the propensity-sanctioning dilemma. How can we sort out the effects of propensity and sanctioning on crime. If either varies, crime changes. By looking at a bivariate probit model, it is possible to make progress in this area. This is an important model for dertermining the effects of imprisonment on crime rates.

Application #3: The Prediction Problem
One of the problems in criminology is the prediction problem. Test-retest correlations of propensity scores are typically above r=.5, often falling in the r=.8 range. However, the best predictors of criminal behavior are limited to an upper range of about r=.4, and often fall in the r=.2 range. How does the apparent stability in traits fit with the apparent instability in behavior? The solution to this dilemma requires an exploration of the state nature of traits.